Created by Browserling
This utility lets you draw custom and colorful canopy fractals. You can change more than a dozen different parameters to create the most pretty trees. You can adjust the bending angle of the right and left branches and set the ratio of their length and thickness from iteration to iteration. For the trunk, you can set its starting width and the growth direction. Optionally, you can disable drawing the trunk altogether and just start with the branches. For the fractal, you can specify the canvas size and add padding around the canopy. As a bonus, you can draw the background and the tree in gradient colors. Fun fact – the pulmonary system used by humans to breathe resembles a fractal canopy. Created by fractal fans from team Browserling. Fractabulous!
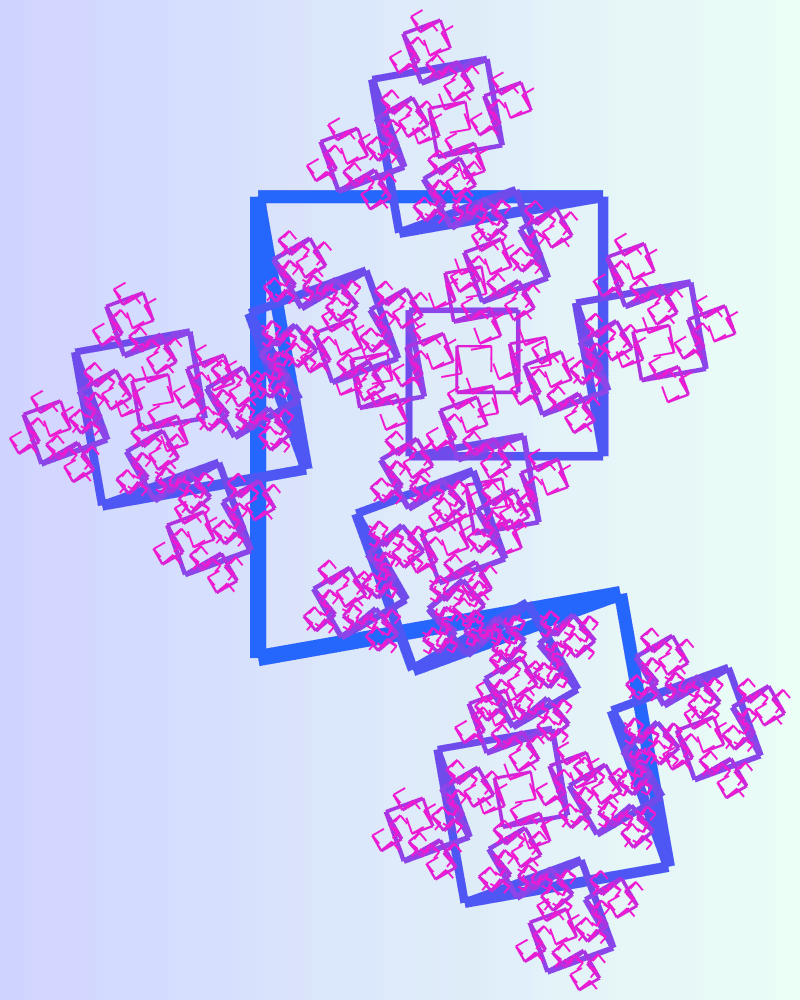
This online browser-based tool illustrates binary fractal trees and their canopies. A fractal canopy is one of many fractals in the family of the tree-like fractals, such as Pythagoras fractal and V-tree. Just like a regular tree, a fractal tree is created by splitting a line segment in two at a certain angle (or two angles – one for each new segment) and with a certain scale factor (or two factors – also one for each new segment). Then each of the two new segments is split again, and again (and again to infinity). If you're thinking in terms of an analogy with a regular tree, then the first line segment is the trunk of the tree, the new split segments are branches, and the final segments at n-th iteration are twigs (also called branch tips). In our tool, each branch can have its own angle that it makes with the trunk. Our tool also has two scale factors that reduce the width and length of the segments in every next iterative step. With every step, twice as many branches bifurcate and the number of branches doubles. We can find that the n-th recursion the tree consists of 2ⁿ - 1 line segments (including the trunk of the tree). If the angle, scale length, and scale width factors of both branches are the same, then we get a symmetric fractal canopy (also known as a symmetric binary fractal tree). Such trees have a left-right symmetry, with the affine hull as the line of reflection. A self-contacting symmetric binary fractal tree has self-intersection but no actual branch crossings. For a given branching angle, there is a unique scaling ratio, such that the corresponding tree is self-contacting. If the branch scale factor is equal to the conjugate of the golden ratio value Φ = 1/φ (where φ = 1.6180339…), then the fractal is called the golden fractal tree, golden canopy or just the golden tree. There are exactly four self-contacting golden trees for which branching angles are 60°, 108°, 120°, and 144°. Angles 90° and 135° are called critical angles of the canopy fractal because at the 90° angle the branches fill the shape of a rectangle, and at the 135° angle, they fill a triangle form. Some combinations of parameters create other well-known fractals, such as Hausdorff tree, Cantor set, and Koch curve, as well as classical geometrical polygons, such as the pentagon and decagon. Mind blowing and ingenious at the same time, or as we love to say – fractabulous!
In this example, we generate the textbook version of the canopy fractal tree. It's symmetric as both of its branches bend at an angle equal to 2π/11 ≈ 16 degrees and both the length and width ratios are 0.75. For the gradient, we've chosen to color each segment level in its own color. The tree starts with the harlequin-green color in the trunk and ends with the blush-pink color in the tips. We bifurcate the tree for 8 iterations and draw it on a cerise-red to Christelle-pink color gradient canvas.
This example sets different bending angles for the segments and as a result, we get a wave-like asymmetrical fractal tree. The left rotation angle is 20 degrees and the right is 90 degrees. It also sets the length factor to 0.7 and the width factor to 0.79. It uses a Portofino-yellow to hit-pink gradient for the background and blue to black gradient for the tree that is applied in the tree's growth direction.
In this example, we draw a canopy that mildly curls in on itself on the right side from below. The angles make 30 and 60 degrees with the direction of the trunk. We generate the tree from a 16-pixel thick trunk and reduce its thickness 0.81 times in every recursion. The lengths of the left and right branches are contracted differently – the left branch decreases by the factor of 0.65 and the right branch by the factor of 0.75. As the right side shrinks slower than the left side, we get a curly tree. We generate 12 recursions on an 800x800 pixel canvas and apply a yellow-blue gradient for the tree from the trunk to the twigs.
In this example, we use a very large bifurcation angle of 345 degrees for the right branch and a right 90-degree angle for the left branch. This makes the fractal heavily tilt to the left. With 12 iteration steps, this behavior makes the branches resemble the wings of a dragonfly. To fit the tree, we have increased the height of the image to 1000 pixels and width to 800 pixels. We fill individual segments with a gradient from selective-yellow color at the ground level to green at the top level.
This example generates a tree with the right angles for both branches. The right angle is the critical angle for a canopy fractal as at this angle it turns in a space-filling fractal and the tree can completely fill a square with its branches. By adjusting the bifurcation scale factors of the curve, we can find values that make the branches not overlap one another, and we get the Hausdorff fractal (also known as the H-tree). We run the iterations for 11 stages and get 2¹¹ - 1 = 2048 - 1 = 2047 segments.
In this example, the canopy looks more like a dragon fractal than a tree fractal. This is due to well-chosen angles for branches (45 and 120 degrees), as well as length scale factors (0.75 and 0.6). We have also activated the "Skip the Trunk" option to make the fractal look more like a dragon. The result that you see is generated via 13 iterative loops and the color gradient we have chosen to fill the curve is lipstick-pink to white.
This is an example of a symmetric binary self-contacting golden fractal tree of 14th order. Let's dissect the meaning of all words used in the title. First, it's symmetric because we use the same bending angle for all branches (equal to 60 degrees). It's binary because it has two branches (there are also other canopies and trees with more branches). Then, it's self-contracting as the twig tips of the left and right branches touch but do not overlay. It's also golden as the branching factor is equal to the value of the golden ratio conjugate Φ = 1/φ = 0.618… (which, surprisingly is also equal to φ-1). Finally, it's the 14th order as it has been iterated 14 times. If you look closely, you can see that the curve on the tree between the rightmost top point and the leftmost top forms a golden Koch curve. But wait, there's more! If you look even more carefully, you'll spot that there's a golden Cantor set hanging in there. The top points of this tree form a middle Cantor set, as is the case for all other self-contacting trees with branching angle less than 135 degrees.
This example also generates a golden self-contacting canopy but here the branch angle is 120 degrees. This tree is filled with an infinite amount of equilateral triangles. One equilateral triangle that you can immediately spot is the smallest triangle that bounds the fractal. The others are hidden in the branches and along the branches. As with the golden 60 canopy (previous example), the top twig points form a hidden Cantor fractal. You can also tile a hexagon with six copies of the canopy as well as create a variation of a Sierpinski triangle with three copies. Last but not least, this fractal also looks like a futuristic lamp post, so if you're designing the next future city, don't forget to credit us for the idea!
In this example, we demonstrate a remarkable variation of a golden self-contacting tree. If the branching angle is 144 degrees, then the tip points of the tree produce the golden Koch fractal. To make the illustration pretty, we turn the fractal upside down, exclude the trunk, and expand the width of the image so that the Koch fractal can be better seen. If four copies of this tree are rotated around the bottom of the trunk with angles that are multiples of 72, then we can also create a golden Koch snowflake.
In this example, we use the following properties for the left and right branches. Left branch: bending angle – 45 degrees, scale factor – 0.7, width factor – 0.83. Right branch: bending angle – 190 degrees, scale factor – 0.6, width factor – also 0.83. With these parameters, the branches of the tree closely twist together, only slightly sprouting to the sides. By generating only 13 iteration steps, we see that the Chinese dragon curve emerges (also known as East Asian dragon). We decorate it with a white-blue gradient flame.
This example generates a square dragon fractal on a rectangular canvas of size 800 by 1000 pixels, with a light gradient from hint-of-green to periwinkle color. It sets the bending angles of the branches to 190 and 90 degrees and sets their scale proportions to 0.6 and 0.75 respectively. It turns the fractal to the left side, removes the padding, and doesn't draw the first segment.
The canopy of this fractal twists so much that it creates a lot of bubble-like structures. Originally, this fractal had no name, so we called it the foamy fractal tree, or foamy canopy for short. To create the bubble effect, we use 72 degrees for the left branch and 188 degrees for the right branch. The reduction factors for both branches is the same. The length reduction factor is equal to 0.69 and the width reduction factor is equal to 0.78. We recurse 13 times and use an azure to white gradient from the trunk to tips.
You can pass options to this tool using their codes as query arguments and it will automatically compute output. To get the code of an option, just hover over its icon. Here's how to type it in your browser's address bar. Click to try!
Quickly draw a custom McWorter dendrite fractal.
Quickly draw a custom canopy tree fractal.
Quickly draw a custom Gosper fractal.
Quickly draw a custom Z-order fractal.
Quickly draw a custom Hilbert fractal.
Quickly draw a custom binary v-fractal.
Quickly draw a custom Peano fractal.
Quickly draw a custom Heighway dragon fractal.
Quickly draw a custom twin dragon Heighway fractal.
Quickly draw a custom Heighway nonadragon fractal.
Quickly draw a custom Koch fractal.
Quickly draw a custom triflake fractal.
Quickly draw a custom Sierpinski triangle fractal.
Quickly draw a custom Sierpinski pentagon fractal.
Quickly draw a custom Sierpinski hexagon fractal.
Quickly draw a custom Sierpinski polygon fractal.
Quickly draw a custom Moore fractal.
Quickly draw a custom Cantor comb fractal.
Quickly draw a custom Cantor dust fractal.
Quickly draw a custom Levy fractal curve.
Quickly draw a custom ice fractal.
Quickly draw a custom Pythagoras tree fractal.
Quickly draw a custom t-square fractal.
Quickly draw a custom Hausdorff tree fractal.
Walk the Hilbert fractal and enumerate its coordinates.
Walk the Peano fractal and enumerate its coordinates.
Walk the Moore fractal and enumerate its coordinates.
Encode the Hilbert fractal as a string.
Encode the Peano fractal as a string.
Encode the Moore fractal as a string.
Encode the Cantor set as a string.
Encode the Heighway Dragon as a string.
Encode the Sierpinski fractal as a string.
Generate a Sierpinski tetrahedron (tetrix) fractal.
Generate a Cantor's cube fractal.
Generate a Sierpinski-Menger fractal.
Generate a Jerusalem cube fractal.
Generate a Jeaninne Mosely fractal.
Generate a Mandelbrot tree fractal.
Generate a Barnsley's tree fractal.
Generate a Barnsley's fern fractal.
Generate a binary tree fractal.
Generate a ternary tree fractal.
Generate a dragon tree fractal.
Generate a de Rham curve.
Generate a Takagi-Landsberg fractal curve.
Generate a Peano pentagon fractal curve.
Generate a tridendrite fractal curve.
Generate a Pentigree fractal curve.
Generate a lucky seven fractal curve.
Generate an Eisenstein fractions fractal curve.
Generate a Bagula double five fractal curve.
Generate a Julia fractal set.
Generate a Mandelbrot fractal set.
Generate a Mandelbulb fractal.
Generate a Mandelbox fractal.
Generate a Buddhabrot fractal.
Generate a Burning Ship fractal.
Generate a toothpick sequence fractal.
Generate an Ulam-Warburton fractal curve.
Generate an ASCII fractal.
Generate an ANSI fractal.
Generate a Unicode fractal.
Generate an emoji fractal.
Generate a braille code fractal.
Generate a fractal in audio form.
Create a fractal that looks like one but isn't a fractal.
Generate a fractal from any text.
Generate a fractal from a string.
Generate a fractal from a number.
Join any two fractals together.
Create a completely random fractal.
Set up an arbitrary IFS system and iterate it.
Recursively transform an image using IFS rules.
Run infinite compositions of analytic functions.
Create a surface that mimics a natural terrain.
Create a fractal surface via Brownian motion.
Apply fractal algorithms on your image and make it self-similar.
Find fractal patterns in any given image.
Find fractal patterns in any given text.
Find fractal patterns in any given number.
Tessellate a plane with fractals.
Run a cellular automaton with custom rules.
Play Conway's Game of Life on an infinite grid.
Subscribe to our updates. We'll let you know when we release new tools, features, and organize online workshops.
Enter your email here